• Table of Contents
• Previous Chapter
• Next Chapter

Chapter 21: Function and Variable Templates

Don't hesitate to send in feedback: send an e-mail if you like the C++ Annotations; if you think that important material was omitted; if you find errors or typos in the text or the code examples; or if you just feel like e-mailing. Send your e-mail to Frank B. Brokken.

Please state the document version you're referring to, as found in the title (in this document: 10.3.0) and please state chapter and paragraph name or number you're referring to.

All received mail is processed conscientiously, and received suggestions for improvements are usually processed by the time a new version of the Annotations is released. Except for the incidental case I will normally not acknowledge the receipt of suggestions for improvements. Please don't interpret this as me not appreciating your efforts.

C++ supports syntactic constructs allowing programmers to define and use completely general (or abstract) functions or classes, based on generic types and/or (possibly inferred) constant values. In the chapters on abstract containers (chapter 12) and the STL (chapter 18) we've already used these constructs, commonly known as the template mechanism.

The template mechanism allows us to specify classes and algorithms, fairly independently of the actual types for which the templates are eventually going to be used. Whenever the template is used, the compiler generates code that is tailored to the particular data type(s) used with the template. This code is generated at compile-time from the template's definition. The piece of generated code is called an instantiation of the template.

In this chapter the syntactic peculiarities of templates are covered. The notions of template type parameter, template non-type parameter, and function template are introduced and several examples of templates are provided (both in this chapter and in chapter 24). Template classes are covered in chapter 22.

Templates already offered by the language include the abstract containers (cf. chapter 12); the string (cf. chapter 5); streams (cf. chapter 6); and the generic algorithms (cf. chapter 19). So, templates play a central role in present-day C++, and should not be considered an esoteric feature of the language.

Templates should be approached somewhat similarly as generic algorithms: they're a way of life; a C++ software engineer should actively look for opportunities to use them. Initially, templates may appear to be rather complex and you might be tempted to turn your back on them. However, over time their strengths and benefits are more and more appreciated. Eventually you'll be able to recognize opportunities for using templates. That's the time where your efforts should no longer focus on constructing ordinary functions and classes (i.e., functions or classes that are not templates), but on constructing templates.

This chapter starts by introducing function templates. The emphasis is on the required syntax. This chapter lays the foundation upon which the other chapters about templates are built.

21.1: Defining function templates

    Type add(Type const &lvalue, Type const &rvalue)
    {
        return lvalue + rvalue;
    }

    int add(int const &lvalue, int const &rvalue)
    {
        return lvalue + rvalue;
    }

    double add(double const &lvalue, double const &rvalue)
    {
        return lvalue + rvalue;
    }

Fortunately, we've already seen an important part of a template function. Our initial function add actually is an implementation of such a function although it isn't a full template definition yet. If we gave the first add function to the compiler, it would produce an error message like:

    error: `Type' was not declared in this scope
    error: parse error before `const'

The full template definition allows for this formal nature of the Type typename. Using the keyword template, we prefix one line to our initial definition, obtaining the following function template definition:

    template <typename Type>
    Type add(Type const &lvalue, Type const &rvalue)
    {
        return lvalue + rvalue;
    }

In this definition we distinguish:

• The keyword template, starting a template definition or declaration.
• The angle bracket enclosed list following template. This is a list containing one or more comma-separated elements. This angle bracket enclosed list is called the template parameter list. Template parameter lists using multiple elements could look like this:

      typename Type1, typename Type2
  

• Inside the template parameter list we find the formal type name Type. It is a formal type name, comparable to a formal parameter name in a function's definition. Up to now we've only encountered formal variable names with functions. The types of the parameters were always known by the time the function was defined. Templates escalate the notion of formal names one step further up the ladder. Templates allow type names to be formalized, rather than just the variable names themselves. The fact that Type is a formal type name is indicated by the keyword typename, prefixed to Type in the template parameter list. A formal type name like Type is also called a template type parameter. Template non-type parameters also exist, and are shortly introduced.

  Other texts on C++ sometimes use the keyword class where we use typename. So, in other texts template definitions might start with a line like:

      template <class Type>
  

  In the C++ Annotations the use of typename over class is preferred, reasoning that a template type parameter is, after all, a type name (some authors prefer class over typename; in the end it's a matter of taste).
• The template keyword and the template parameter list is called the template header.
• The function head: it is like a normal function head, albeit that the template's type parameters must be used in its parameter list. When the function is eventually called using actual arguments having actual types, these actual types are used by the compiler to infer which version (i.e., overload to fit the actual argument types) of the function template must be used. At the point where the function is called the compiler creates the function that is called, a process called instantiation. The function head may also use a formal type to specify its return value. This feature was actually used in the add template's definition.
• The function parameters are specified as Type const & parameters. This has the usual meaning: the parameters are references to Type objects or values that will not be modified by the function.
• The function body is like a normal function body. In the body the formal type names may be used to define or declare variables, which may then be used as any other local variable. But some restrictions apply. Looking at add's body, it is clear that operator+ is used, as well as a copy constructor, as the function returns a value. This allows us to formulate the following restrictions for the formal type Type as used by our add function template:
  • Type should support operator+
  • Type should support a copy constructor
  Consequently, while Type could be a string, it could never be an ostream, as neither operator+ nor the copy constructor are available for streams.

21.1.1: Considerations regarding template parameters

    template <typename Type>
    Type add(Type const &lvalue, Type const &rvalue)
    {
        return lvalue + rvalue;
    }

Look again at add's parameters. By specifying Type const & rather than Type superfluous copying is prevented, at the same time allowing values of primitive types to be passed as arguments to the function. So, when add(3, 4) is called, int{4} is assigned to Type const &rvalue. In general, function parameters should be defined as Type const & to prevent unnecessary copying. The compiler is smart enough to handle `references to references' in this case, which is something the language normally does not support. For example, consider the following main function (here and in the following simple examples it is assumed that the template and the required headers and namespace declarations have been provided):

    int main()
    {
        size_t const &var = size_t{4};
        cout << add(var, var) << '\n';
    }

    int main()
    {
        cout << add(string{"a"}, string{"b"}) << '\n';
    }

    int main()
    {
        string const &s = string{"a"};
        cout << add(s, s) << '\n';
    }

• In general, function parameters should be specified as Type const & parameters to prevent unnecessary copying.
• The template mechanism is fairly flexible. Formal types are interpreted as plain types, const types, pointer types, etc., depending on the actually provided types. The rule of thumb is that the formal type is used as a generic mask for the actual type, with the formal type name covering whatever part of the actual type must be covered. Some examples, assuming the parameter is defined as Type const &:

  Provided argument:	Actually used Type:
  size_t const	size_t
  size_t	size_t
  size_t *	size_t *
  size_t const *	size_t const *

    template <typename Type, size_t Size>
    Type sum(Type const (&array)[Size])
    {
        Type tp{};  // note: the default constructor must exist.

        for (size_t idx = 0; idx < Size; idx++)
            tp += array[idx];

        return tp;
    }

• The template parameter list. This template parameter list has two elements. The first element is a well-known template type parameter, but the second element has a very specific type: a size_t. Template parameters of specific (i.e., non-formal) types used in template parameter lists are called template non-type parameters. A template non-type parameter defines the type of a constant expression, which must be known by the time the template is instantiated and which is specified in terms of existing types, such as a size_t.
• Looking at the function's head, we see one parameter:

  Type const (&array)[Size]
  

  This parameter defines array as a reference to an array having Size elements of type Type that may not be modified.
• In the parameter definition, both Type and Size are used. Type is of course the template's type parameter Type, but Size is also a template parameter. It is a size_t, whose value must be inferable by the compiler when it compiles an actual call of the sum function template. Consequently, Size must be a const value. Such a constant expression is called a template non-type parameter, and its type is named in the template's parameter list.
• When the function template is called, the compiler must be able to infer not only Type's concrete value, but also Size's value. Since the function sum only has one parameter, the compiler is only able to infer Size's value from the function's actual argument. It can do so if the provided argument is an array (of known and fixed size) rather than a pointer to Type elements. So, in the following main function the first statement will compile correctly but the second statement will not:

  int main()
  {
      int values[5];
      int *ip = values;
  
      cout << sum(values) << '\n';    // compiles OK
      cout << sum(ip) << '\n';        // won't compile
  }
  

• Inside the function's body the statement Type tp = Type() is used to initialize tp to a default value. Note here that no fixed value (like 0) is used. Any type's default value may be obtained using its default constructor rather than using a fixed numeric value. Of course, not every class accepts a numeric value as an argument to one of its constructors. But all types, even the primitive types, support default constructors (actually, some classes do not implement a default constructor, or make it inaccessible; but most do). The default constructor of primitive types initializes their variables to 0 (or false). Furthermore, the statement Type tp = Type() is a true initialization: tp is initialized by Type's default constructor, rather than using Type's copy constructor to assign Type's copy to tp.

  It's interesting to note here (although not directly related to the current topic) that the syntactic construction Type tp(Type()) cannot be used, even though it also looks like a proper initialization. Usually an initializing argument can be provided to an object's definition, like string s("hello"). Why, then, is Type tp = Type() accepted, whereas Type tp(Type()) isn't? When Type tp(Type()) is used it won't result in an error message. So we don't immediately detect that it's not a Type object's default initialization. Instead, the compiler starts generating error messages once tp is used. This is caused by the fact that in C++ (and in C alike) the compiler does its best to recognize a function or function pointer whenever possible: the function prevalence rule. According to this rule Type() is (because of the pair of parentheses) interpreted as a pointer to a function expecting no arguments; returning a Type. The compiler will do so unless it clearly isn't possible to do so. In the initialization Type tp = Type() it can't see a pointer to a function as a Type object cannot be given the value of a function pointer (remember: Type() is interpreted as Type (*)() whenever possible). But in Type tp(Type()) it can use the pointer interpretation: tp is now declared as a function expecting a pointer to a function returning a Type, with tp itself also returning a Type. E.g., tp could have been defined as:

  Type tp(Type (*funPtr)())
  {
      return (*funPtr)();
  }
  

• Comparable to the first function template, sum also assumes the existence of certain public members in Type's class. This time operator+= and Type's copy constructor.

Like class definitions, template definitions should not contain using directives or declarations: the template might be used in a situation where such a directive overrides the programmer's intentions: ambiguities or other conflicts may result from the template's author and the programmer using different using directives (E.g, a cout variable defined in the std namespace and in the programmer's own namespace). Instead, within template definitions only fully qualified names, including all required namespace specifications should be used.

21.1.2: Late-specified return type

    int add(int lhs, int rhs)
    {
        return lhs + rhs;
    }

    template <typename Lhs, typename Rhs>
    Lhs add(Lhs lhs, Rhs rhs)
    {
        return lhs + rhs;
    }

    add(3, 3.4)

    add<double>(3, 3.4);

    template <typename Lhs, typename Rhs>
    decltype(lhs + rhs) add(Lhs lhs, Rhs rhs)
    {
        return lhs + rhs;
    }

The decltype-based definition of a function's return type may become fairly complex. This complexity can be reduced by using the late-specified return type syntax that does allow the use of decltype to define a function's return type. It is primarily used with function templates but it may also be used for ordinary (non-template) functions:

    template <typename Lhs, typename Rhs>
    auto add(Lhs lhs, Rhs rhs) -> decltype(lhs + rhs)
    {
        return lhs + rhs;
    }

    template <typename T, typename U>
    decltype((*(T*)0)+(*(U*)0)) add(T t, U u);

    template <typename T, typename U>
    auto add(T t, U u) -> decltype(t+u);

The expression specified with decltype does not necessarily use the parameters lhs and rhs themselves. In the next function definition lhs.length is used instead of lhs itself:

    template <typename Class, typename Rhs>
    auto  add(Class lhs, Rhs rhs) -> decltype(lhs.length() + rhs)
    {
        return lhs.length() + rhs;
    }

    std::string global;

    template <typename MEMBER, typename RHS>
    auto  add(MEMBER mem, RHS rhs) -> decltype((global.*mem)() + rhs)
    {
        return (global.*mem)() + rhs;
    }

21.2: Passing arguments by reference (reference wrappers)

Situations exist where the compiler is unable to infer that a reference rather than a value is passed to a function template. In the following example the function template outer receives int x as its argument and the compiler dutifully infers that Type is int:

    template <typename Type>
    void outer(Type t)
    {
        t.x();
    }
    void useInt()
    {
        int arg;
        outer(arg);
    }

Compilation will of course fail and the compiler nicely reports the inferred type, e.g.:

    In function 'void outer(Type) [with Type = int]': ...

Unfortunately the same error is generated when using call in the next example. The function call is a template expecting a function that takes an argument which is then itself modified, and a value to pass on to that function. Such a function is, e.g., sqrtArg expecting a reference to a double, which is modified by calling std::sqrt.

    void sqrtArg(double &arg)
    {
        arg = sqrt(arg);
    }
    template<typename Fun, typename Arg>
    void call(Fun fun, Arg arg)
    {
        fun(arg);
        cout << "In call: arg = " << arg << '\n';
    }

Assuming double value = 3 then call(sqrtArg, value) does not modify value as the compiler infers Arg to be double and hence passes value by value.

To have value itself changed the compiler must be informed that value must be passed by reference. Note that it might not be acceptable to define call's template argument as Arg & as not changing the actual argument might be appropriate in some situations.

The ref(arg) and cref(arg) reference wrappers can be used. They accept an argument and return it as a (const) reference-typed argument. To actually change value it can be passed to call using ref(value) as shown in the following main function:

    int main()
    {
        double value = 3;
        call(sqrtArg, value);
        cout << "Passed value, returns: " << value << '\n';

        call(sqrtArg, ref(value));
        cout << "Passed ref(value), returns: " << value << '\n';
    }
    /*
        Displays:
            In call: arg = 1.73205
            Passed value, returns: 3
            In call: arg = 1.73205
            Passed ref(value), returns: 1.73205
    */

21.3: Using local and unnamed types as template arguments

    enum
    {
        V1,
        V2,
        V3
    };

When defining a function template, the compiler normally deducts the types of its template type parameters from its arguments:

    template <typename T>
    void fun(T &&t);

    fun(3);     // T is int
    fun('c');   // T is char

    fun(V1);    // T is a value of the above enum type

    template <typename T>
    void fun(T &&t)
    {
        T var(t);
    }

Values or objects of locally defined types may also be passed as arguments to function templates. E.g.,

    void definer()
    {
        struct Local
        {
            double  dVar;
            int     iVar;
        };
        Local local;            // using a local type

        fun(local);             // OK: T is 'Local'
    }

21.4: Template parameter deduction

When the compiler deduces the actual types for template type parameters it only considers the types of the arguments that are actually used. Neither local variables nor the function's return value is considered in this process. This is understandable. When a function is called the compiler is only certain about the types of the function template's arguments. At the point of the call it definitely does not see the types of the function's local variables. Also, the function's return value might not actually be used or may be assigned to a variable of a subrange (or super-range) type of a deduced template type parameter. So, in the following example, the compiler won't ever be able to call fun(), as it won't be able to deduce the actual type for the Type template type parameter.

    template <typename Type>
    Type fun()              // can never be called as `fun()'
    {
        return Type{};
    }

In general, when a function has multiple parameters of identical template type parameters, the actual types must be exactly the same. So, whereas

    void binarg(double x, double y);

    template <typename Type>
    void binarg(Type const &p1, Type const &p2)
    {}

    int main()
    {
        binarg(4, 4.5); // ?? won't compile: different actual types
    }

What, then, are the transformations the compiler applies when deducing the actual types of template type parameters? It performs but three types of parameter type transformations and a fourth one to function template non-type parameters. If it cannot deduce the actual types using these transformations, the function template will not be considered. The transformations performed by the compiler are:

• lvalue transformations, creating an rvalue from an lvalue;
• qualification transformations, inserting a const modifier to a non-constant argument type;
• transformation to a base class instantiated from a class template, using a template base class when an argument of a template derived class type was provided in the call.
• Standard transformations for function template non-type parameters. This isn't a template type parameter transformation, but it refers to any remaining template non-type parameter of function templates. For these function parameters the compiler performs any standard conversion it has available (e.g., int to size_t, int to double, etc.).

21.4.1: Lvalue transformations

• lvalue-to-rvalue transformations.

  An lvalue-to-rvalue transformation is applied when an rvalue is required, but an lvalue is provided. This happens when a variable is used as argument to a function specifying a value parameter. For example,

  template<typename Type>
  Type negate(Type value)
  {
      return -value;
  }
  int main()
  {
      int x = 5;
      x = negate(x);  // lvalue (x) to rvalue (copies x)
  }
  

• array-to-pointer transformations.

  An array-to-pointer transformation is applied when the name of an array is assigned to a pointer variable. This is frequently used with functions defining pointer parameters. Such functions frequently receive arrays as their arguments. The array's address is then assigned to the pointer-parameter and its type is used to deduce the corresponding template parameter's type. For example:

  template<typename Type>
  Type sum(Type *tp, size_t n)
  {
      return accumulate(tp, tp + n, Type());
  }
  int main()
  {
      int x[10];
      sum(x, 10);
  }
  

  In this example, the location of the array x is passed to sum, expecting a pointer to some type. Using the array-to-pointer transformation, x's address is considered a pointer value which is assigned to tp, deducing that Type is int in the process.

• function-to-pointer transformations.

  This transformation is most frequently used with function templates defining a parameter which is a pointer to a function. When calling such a function the name of a function may be specified as its argument. The address of the function is then assigned to the pointer-parameter, deducing the template type parameter in the process. This is called a function-to-pointer transformation. For example:

  #include <cmath>
  
  template<typename Type>
  void call(Type (*fp)(Type), Type const &value)
  {
      (*fp)(value);
  }
  int main()
  {
      call(sqrt, 2.0);
  }
  

  In this example, the address of the sqrt function is passed to call, expecting a pointer to a function returning a Type and expecting a Type for its argument. Using the function-to-pointer transformation, sqrt's address is assigned to fp, deducing that Type is double in the process (note that sqrt is the address of a function, not a variable that is a pointer to a function, hence the lvalue transformation).

  The argument 2.0 could not have been specified as 2 as there is no int sqrt(int) prototype. Furthermore, the function's first parameter specifies Type (*fp)(Type), rather than Type (*fp)(Type const &) as might have been expected from our previous discussion about how to specify the types of function template's parameters, preferring references over values. However, fp's argument Type is not a function template parameter, but a parameter of the function fp points to. Since sqrt has prototype double sqrt(double), rather than double sqrt(double const &), call's parameter fp must be specified as Type (*fp)(Type). It's that strict.

21.4.2: Qualification transformations

    template<typename Type>
    Type negate(Type const &value)
    {
        return -value;
    }
    int main()
    {
        int x = 5;
        x = negate(x);
    }

21.4.3: Transformation to a base class

In section 22.11 it is shown how a class template can be derived from another class template.

As class template derivation remains to be covered, the following discussion is necessarily somewhat premature. The reader may of course skip briefly to section 22.11 returning back to this section thereafter.

In this section it should be assumed, for the sake of argument, that a class template Vector has somehow been derived from a std::vector. Furthermore, assume that the following function template has been constructed to sort a vector using some function object obj:

    template <typename Type, typename Object>
    void sortVector(std::vector<Type> vect, Object const &obj)
    {
        sort(vect.begin(), vect.end(), obj);
    }

    class CaseLess
    {
        public:
            bool operator()(std::string const &before,
                            std::string const &after) const
            {
                return strcasecmp(before.c_str(), after.c_str()) < 0;
            }
    };

    int main()
    {
        std::vector<string> vs;
        std::vector<int> vi;

        sortVector(vs, CaseLess());
        sortVector(vi, less<int>());
    }

    int main()
    {
        Vector<string> vs;      // `Vector' instead of `std::vector'
        Vector<int> vi;

        sortVector(vs, CaseLess());
        sortVector(vi, less<int>());
    }

21.4.4: The template parameter deduction algorithm

• In turn, the function template's parameters are identified using the arguments of the called function.
• For each template parameter used in the function template's parameter list, the template type parameter is associated with the corresponding argument's type (e.g., Type is int if the argument is int x, and the function's parameter is Type &value).
• While matching the argument types to the template type parameters, the three allowed transformations (see section 21.4) for template type parameters are applied where necessary.
• If identical template type parameters are used with multiple function parameters, the deduced template types must exactly match. So, the next function template cannot be called with an int and a double argument:

  template <typename Type>
  Type add(Type const &lvalue, Type const &rvalue)
  {
      return lvalue + rvalue;
  }
  

  When calling this function template, two identical types must be used (albeit that the three standard transformations are of course allowed). If the template deduction mechanism does not come up with identical actual types for identical template types, then the function template is not going to be instantiated.

21.4.5: Template type contractions

In such cases the compiler performs type contractions. Doubling identical reference types results in a simple contraction: the type is deduced to be a single reference type. Example: if the template parameter type is specified as a Type && and the actual parameter is an int && then Type is deduced to be an int, rather than an int &&.

This is fairly intuitive. But what happens if the actual type is int &? There is no such thing as an int & &&param and so the compiler contracts the double reference by removing the rvalue reference, keeping the lvalue reference. Here the following rules are applied:

1. A function template parameter defined as an lvalue reference to a template's type parameter (e.g., Type &) receiving an lvalue reference argument results in a single lvalue reference.

2. A function template parameter defined as an rvalue reference to a template's type parameter (e.g., Type &&) receiving any kind of reference argument uses the reference type of the argument.

• When providing an Actual & argument then Type & becomes an Actual & and Type is inferred as Actual;

• When providing an Actual & then Type && becomes an Actual & and Type is inferred as Actual;

• When providing an Actual && then Type & also becomes Actual & and Type is inferred as Actual;

• When providing an Actual && then Type && becomes Actual && and Type is inferred as Actual;

Let's look at a concrete exampe where contraction occurs. Consider the following function template where a function parameter is defined as an rvalue references to some template type parameter:

    template <typename Type>
    void function(Type &&param)
    {
        callee(static_cast<Type &&>(param));
    }

Likewise, when callee is called using the static_cast the same contraction occurs, so Type &&param operates on Tp &param. Therefore (using contraction) the static cast also uses type Tp &param. If param happened to be of type Tp && then the static cast uses type Tp &&param.

This characteristic allows us to pass a function argument to a nested function without changing its type: lvalues remain lvalues, rvalues remain rvalues. This characteristic is therefore also known as perfect forwarding which is discussed in greater detail in section 22.5.2. Perfect forwarding prevents the template author from having to define multiply overloaded versions of a function template.

21.5: Declaring function templates

• Like class interfaces, template definitions are usually included in header files. Every time a header file containing a template definition is read by the compiler it must process the full definition. It must do so even if it does not actually use the template. This somewhat slows-down the compilation. For example, compiling a template header file like algorithm on my old laptop takes about four times the amount of time it takes to compile a plain header file like cmath. The header file iostream is even harder to process, requiring almost 15 times the amount of time it takes to process cmath. Clearly, processing templates is serious business for the compiler. On the other hand this drawback shouldn't be taken too seriously. Compilers are continuously improving their template processing capacity and computers keep getting faster and faster. What was a nuisance a few years ago is hardly noticeable today.
• Every time a function template is instantiated, its code appears in the resulting object module. However, if multiple instantiations of a template using the same actual types for its template parameters exist in multiple object files the one definition rule is lifted. The linker weeds out superfluous instantiations (i.e., identical definitions of instantiated templates). In the final program only one instantiation for a particular set of actual template type parameters remain available (see section 21.6 for an illustration). Therefore, the linker has an additional task to perform (viz. weeding out multiple instantiations), which somewhat slows down the linking process.
• Sometimes the definitions themselves are not required, but references or pointers to the templates are. Requiring the compiler to process the full template definitions in those cases needlessly slows down the compilation process.
• In the context of template meta programming (see chapter 23) it is sometimes not even required to provide a template implementation. Instead, only specializations (cf. section 21.9) are created which are based upon the mere declaration.

When templates are declared, the compiler does not have to process the template's definitions again and again; and no instantiations are created on the basis of template declarations alone. Any actually required instantiation must then be available elsewhere (of course, this holds true for declarations in general). Unlike the situation we encounter with ordinary functions, which are usually stored in libraries, it is currently not possible to store templates in libraries (although the compiler may construct precompiled header files). Consequently, using template declarations puts a burden on the shoulders of the software engineer, who has to make sure that the required instantiations exist. Below a simple way to accomplish that is introduced.

To create a function template declaration simply replace the function's body by a semicolon. Note that this is exactly identical to the way ordinary function declarations are constructed. So, the previously defined function template add can simply be declared as

    template <typename Type>
    Type add(Type const &lvalue, Type const &rvalue);

    std::string getCsvLine(std::istream &in, char const *delim);

    #include <iosfwd>

21.5.1: Instantiation declarations

For this a variant of a template declaration is available, a so-called explicit instantiation declaration. An explicit instantiation declaration consists of the following elements:

• It starts with the keyword template, omitting the template parameter list.
• Next the function template's return type and name are specified.
• The function template's name is followed by a type specification list. A type specification list is an angle brackets enclosed list of type names. Each type specifies the actual type of the corresponding template type parameter in the template's parameter list.
• Finally the function template's parameter list is specified, terminated by a semicolon.

Using explicit instantiation declarations all instantiations of template functions required by a program can be collected in one file. This file, which should be a normal source file, should include the template definition header file and should subsequently specify the required explicit instantiation declarations. Since it's a source file, it is not included by other sources. So namespace using directives and declarations may safely be used once the required headers have been included. Here is an example showing the required instantiations for our earlier add function template, instantiated for double, int, and std::string types:

    #include "add.h"
    #include <string>
    using namespace std;

    template int add<int>(int const &lvalue, int const &rvalue);
    template double add<double>(double const &lvalue, double const &rvalue);
    template string add<string>(string const &lvalue, string const &rvalue);

21.6: Instantiating function templates

So, when is a function template actually instantiated? There are two situations where the compiler decides to instantiate templates:

• They are instantiated when they are used (e.g., the function add is called with a pair of size_t values);
• When addresses of function templates are taken they are instantiated. Example:

  char (*addptr)(char const &, char const &) = add;
  

The compiler is not always able to deduce the template's type parameters unambiguously. When the compiler reports an ambiguity it must be solved by the software engineer. Consider the following code:

    #include <iostream>
    #include "add.h"

    size_t fun(int (*f)(int *p, size_t n));
    double fun(double (*f)(double *p, size_t n));

    int main()
    {
        std::cout << fun(add);
    }

When this little program is compiled, the compiler reports an ambiguity it cannot resolve. It has two candidate functions as for each overloaded version of fun an add function can be instantiated:

    error: call of overloaded 'fun(<unknown type>)' is ambiguous
    note: candidates are: int fun(size_t (*)(int*, size_t))
    note:                 double fun(double (*)(double*, size_t))

    #include <iostream>
    #include "add.h"

    int fun(int (*f)(int const &lvalue, int const &rvalue));
    double fun(double (*f)(double const &lvalue, double const &rvalue));

    int main()
    {
        std::cout << fun(
                        static_cast<int (*)(int const &, int const &)>(add)
                    );
    }

But it's good practice to avoid type casts wherever possible. How to do this is explained in the next section (21.7).

21.6.1: Instantiations: no `code bloat'

• First we construct several source files:
  • source1.cc defines a function fun, instantiating add for int-type arguments, including add's template definition. It displays add's address:

        union PointerUnion
        {
            int (*fp)(int const &, int const &);
            void *vp;
        };
    

        #include <iostream>
        #include "add.h"
        #include "pointerunion.h"
    
        void fun()
        {
            PointerUnion pu = { add };
    
            std::cout << pu.vp << '\n';
        }
    

  • source2.cc defines the same function, but merely declares the proper add template using a template declaration (not an instantiation declaration). Here is source2.cc:

        #include <iostream>
        #include "pointerunion.h"
    
        template<typename Type>
        Type add(Type const &, Type const &);
    
        void fun()
        {
            PointerUnion pu = { add };
    
            std::cout << pu.vp << '\n';
        }
    

  • main.cc again includes add's template definition, declares the function fun and defines main, defining add for int-type arguments as well and displaying add's function address. It also calls the function fun. Here is main.cc:

        #include <iostream>
        #include "add.h"
        #include "pointerunion.h"
    
        void fun();
    
        int main()
        {
            PointerUnion pu = { add };
    
            fun();
            std::cout << pu.vp << '\n';
        }
    

• All sources are compiled to object modules. Note the different sizes of source1.o (1912 bytes using g++ version 4.3.4 (sizes of object modules reported in this section may differ for different compilers and/or run-time libraries)) and source2.o (1740 bytes). Since source1.o contains the instantiation of add, it is somewhat larger than source2.o, containing only the template's declaration. Now we're ready to start our little experiment.
• Linking main.o and source1.o, we obviously link together two object modules, each containing its own instantiation of the same template function. The resulting program produces the following output:

      0x80486d8
      0x80486d8
  

  Furthermore, the size of the resulting program is 6352 bytes.
• Linking main.o and source2.o, we now link together an object module containing the instantiation of the add template, and another object module containing the mere declaration of the same template function. So, the resulting program cannot but contain a single instantiation of the required function template. This program has exactly the same size, and produces exactly the same output as the first program.

21.7: Using explicit template types

With function templates static casts may indeed be avoided using explicit template type arguments. Explicit template type arguments can be used to inform the compiler about the actual types it should use when instantiating a template. To use explicit type arguments the function's name is followed by an actual template type argument list which may again be followed by the function's argument list. The actual types mentioned in the actual template argument list are used by the compiler to `deduce' what types to use when instantiating the template. Here is the example from the previous section, now using explicit template type arguments:

    #include <iostream>
    #include "add.h"

    int fun(int (*f)(int const &lvalue, int const &rvalue));
    double fun(double (*f)(double const &lvalue, double const &rvalue));

    int main()
    {
        std::cout << fun(add<int>) << '\n';
    }

Explicit template type arguments can be used in situations where the compiler has no way to detect which types should actually be used. E.g., in section 21.4 the function template Type fun() was defined. To instantiate this function for the double type, we can call fun<double>().

21.8: Overloading function templates

    int main()
    {
        add(add(2, 3), 4);
    }

To define an overloaded function template, merely put multiple definitions of the template in its header file. For the add function this would boil down to:

    template <typename Type>
    Type add(Type const &lvalue, Type const &rvalue)
    {
        return lvalue + rvalue;
    }
    template <typename Type>
    Type add(Type const &lvalue, Type const &mvalue, Type const &rvalue)
    {
        return lvalue + mvalue + rvalue;
    }

    template <typename Type>
    Type add(std::vector<Type> const &vect)
    {
        return accumulate(vect.begin(), vect.end(), Type());
    }

When overloading function templates we do not have to restrict ourselves to the function's parameter list. The template's type parameter list itself may also be overloaded. The last definition of the add template allows us to specify a vector as its first argument, but no deque or map. Overloaded versions for those types of containers could of course be constructed, but how far should we go? A better approach seems to be to look for common characteristics of these containers. If found we may be able to define an overloaded function template based on these common characteristics. One common characteristic of the mentioned containers is that they all support begin and end members, returning iterators. Using this, we could define a template type parameter representing containers that must support these members. But mentioning a plain `container type' doesn't tell us for what type of data it was instantiated. So we need a second template type parameter representing the container's data type, thus overloading the template's type parameter list. Here is the resulting overloaded version of the add template:

    template <typename Container, typename Type>
    Type add(Container const &cont, Type const &init)
    {
        return std::accumulate(cont.begin(), cont.end(), init);
    }

    template <typename Type, typename Container>
    Type add(Container const &cont)
    {
        return std::accumulate(cont.begin(), cont.end(), Type());
    }

    int x = add(vectorOfInts);

    int x = add<int>(vectorOfInts);

21.8.1: An example using overloaded function templates

    using namespace std;

    int main()
    {
        vector<int> v;

        add(3, 4);          // 1 (see text)
        add(v);             // 2
        add(v, 0);          // 3
    }

• In statement 1 the compiler recognizes two identical types, both int. It therefore instantiates add<int>, our very first definition of the add template.
• In statement 2 a single argument is used. Consequently, the compiler looks for an overloaded version of add requiring but one argument. It finds the overloaded function template expecting a std::vector, deducing that the template's type parameter must be int. It instantiates

      add<int>(std::vector<int> const &)
  

• In statement 3 the compiler again encounters an argument list having two arguments. However, this time the types of the arguments aren't equal, so add template's first definition can't be used. But it can use the last definition, expecting entities having different types. As a std::vector supports begin and end, the compiler is now able to instantiate the function template

  add<std::vector<int>, int>(std::vector<int> const &, int const &)
  

21.8.2: Ambiguities when overloading function templates

    #include "add.h"

    template <typename T1, typename T2>
    T1 add(T1 const &lvalue, T2 const &rvalue)
    {
        return lvalue + rvalue;
    }
    int main()
    {
        add(3, 4.5);
    }

        error: call of overloaded `add(int, double)' is ambiguous
        error: candidates are: Type add(const Container&, const Type&)
                                    [with Container = int, Type = double]
        error:                 T1 add(const T1&, const T2&)
                                    [with T1 = int, T2 = double]

    template <typename Type>
    Type add(Type const &lvalue, Type const &mvalue, Type const &rvalue)
    {
        return lvalue + mvalue + rvalue;
    }

    template <typename Type1, typename Type2, typename Type3>
    Type1 add(Type1 const &lvalue, Type2 const &mvalue, Type3 const &rvalue)
    {
        return lvalue + mvalue + rvalue;
    }

    add(1, 2, 3);

No ambiguity is reported because of the following. If overloaded template functions are defined using less and more specialized template type parameters (e.g., less specialized: all types different vs. more specialized: all types equal) then the compiler selects the more specialized function whenever possible.

As a rule of thumb: overloaded function templates must allow a unique combination of template type arguments to be specified to prevent ambiguities when selecting which overloaded function template to instantiate. The ordering of template type parameters in the function template's type parameter list is not important. E.g., trying to instantiate one of the following function templates results in an ambiguity:

    template <typename T1, typename T2>
    void binarg(T1 const &first, T2 const &second)
    {}
    template <typename T1, typename T2>
    void binarg(T2 const &first, T1 const &second)
    {}

21.8.3: Declaring overloaded function templates

• To declare a function template add accepting certain containers:

  template <typename Container, typename Type>
  Type add(Container const &container, Type const &init);
  

• to use an instantiation declaration (in which case the compiler must already have seen the template's definition):

  template int add<std::vector<int>, int>
                  (std::vector<int> const &vect, int const &init);
  

• to use explicit template type arguments:

  std::vector<int> vi;
  int sum = add<std::vector<int>, int>(vi, 0);
  

21.9: Specializing templates for deviating types

In such situations the compiler may be able to resolve the template type parameters but it (or we ...) may then detect that the standard implementation is pointless or produces errors.

To solve this problem a template explicit specialization may be defined. A template explicit specialization defines the function template for which a generic definition already exists using specific actual template type parameters. As we saw in the previous section the compiler always prefers a more specialized function over a less specialized one. So the template explicit specialization is selected whenever possible.

A template explicit specialization offers a specialization for its template type parameter(s). The special type is consistently subsituted for the template type parameter in the function template's code. For example if the explicitly specialized type is char const * then in the template definition

    template <typename Type>
    Type add(Type const &lvalue, Type const &rvalue)
    {
        return lvalue + rvalue;
    }

    char const *add(char const *const &lvalue, char const *const &rvalue);

    int main(int argc, char **argv)
    {
        add(argv[0], argv[1]);
    }

To see what happened here we replay, step by step, the compiler's actions:

• add is called with char * arguments.
• Both types are equal, so the compiler deduces that Type equals char *.
• Now it inspects the specialization. Can a char * template type argument match a char const *const & template parameter? Here opportunities for the allowable transformations from section 21.4 may arise. A qualification transformation seems to be the only viable one, allowing the compiler to bind a const-parameter to a non-const argument.
• So, in terms of Type the compiler can match an argument of some Type or an argument of some Type const to a Type const &.
• Type itself is not modified, and so Type is a char *.
• Next the compiler inspects the available explicit specializations. It finds one, specializing for char const *.
• Since a char const * is not a char * it rejects the explicit specialization and uses the generic form, resulting in a compilation error.

    char *add(char *const &lvalue, char *const &rvalue);

Instead of defining another explicit specialization an overloaded function template could be designed expecting pointers. The following function template definition expects two pointers to constant Type values and returns a pointer to a non-constant Type:

    template <typename Type>
    Type *add(Type const *t1, Type const *t2)
    {
        std::cout << "Pointers\n";
        return new Type;
    }

As the above overloaded function template only accepts char const * arguments, it will not accept (without a reinterpret cast) char * arguments. So main's argv elements cannot be passed to our overloaded function template.

21.9.1: Avoiding too many specializations

In some situations constructing template explicit specialization may of course be defensible. Two specializations for const and non-const pointers to characters might be appropriate for our add function template. Here's how they are constructed:

• Start with the keyword template.
• Next, an empty set of angle brackets is written. This indicates to the compiler that there must be an existing template whose prototype matches the one we're about to define. If we err and there is no such template then the compiler reports an error like:

      error: template-id `add<char*>' for `char* add(char* const&, char*
             const&)' does not match any template declaration
  

• Now the function's head is defined. It must match the prototype of the initial function template or the form of a template explicit instantiation declaration (see section 21.5.1) if its specialized type cannot be determined from the function's arguments. It must specify the correct returntype, function name, maybe explicit template type arguments, as well as the function's parameter list.
• Finally the function's body is defined, providing the special implementation that is required for the specialization.

Here are two explicit specializations for the function template add, expecting char * and char const * arguments:

    template <> char *add<char *>(char *const &p1,
                                        char *const &p2)
    {
        std::string str(p1);
        str += p2;
        return strcpy(new char[str.length() + 1], str.c_str());
    }

    template <> char const *add<char const *>(char const *const &p1,
                                        char const *const &p2)
    {
        static std::string str;
        str = p1;
        str += p2;
        return str.c_str();
    }

21.9.2: Declaring specializations

When declaring a template explicit specialization the pair of angle brackets following the template keyword are essential. If omitted, we would have constructed a template instantiation declaration. The compiler would silently process it, at the expense of a somewhat longer compilation time.

When declaring a template explicit specialization (or when using an instantiation declaration) the explicit specification of the template type parameters can be omitted if the compiler is able to deduce these types from the function's arguments. As this is the case with the char (const) * specializations, they could also be declared as follows:

    template <> char *add(char *const &p1, char *const &p2)
    template <> char const *add(char const *const &p1,
                                char const *const &p2);

A function template explicit specialization is not just another overloaded version of the function template. Whereas an overloaded version may define a completely different set of template parameters, a specialization must use the same set of template parameters as its non-specialized variant. The compiler uses the specialization in situations where the actual template arguments match the types defined by the specialization (following the rule that the most specialized set of parameters matching a set of arguments will be used). For different sets of parameters overloaded versions of functions (or function templates) must be used.

21.9.3: Complications when using the insertion operator

A conversion operator is guaranteed to be used as an rvalue. This means that objects of a class defining a string conversion operator can be assigned to, e.g., string objects. But when trying to insert objects defining string conversion operators into streams then the compiler complains that we're attemping to insert an inappropriate type into an ostream.

On the other hand, when this class defines an int conversion operator insertion is performed flawlessly.

The reason for this distinction is that operator<< is defined as a plain (free) function when inserting a basic type (like int) but it is defined as a function template when inserting a string. Hence, when trying to insert an object of our class defining a string conversion operator the compiler visits all overloaded versions of insertion operators inserting into ostream objects.

Since no basic type conversion is available the basic type insertion operators can't be used. Since the available conversions for template arguments do not allow the compiler to look for conversion operators our class defining the string conversion operator cannot be inserted into an ostream.

If it should be possible to insert objects of such a class into ostream objects the class must define its own overloaded insertion operator (in addition to the string conversion operator that was required to use the class's objects as rvalue in string assignments).

21.10: Static assertions

    static_assert(constant expression, error message)

    static_assert(BUFSIZE1 == BUFSIZE2,
                                "BUFSIZE1 and BUFSIZE2 must be equal");

    template <typename Type1, typename Type2>
    void rawswap(Type1 &type1, Type2 &type2)
    {
        static_assert(sizeof(Type1) == sizeof(Type2),
                        "rawswap: Type1 and Type2 must have equal sizes");
        // ...
    }

The second example shows how static_assert can be used to ensure that a template operates under the right condition(s).

The string defined in static_assert's second argument is displayed and compilation stops if the condition specified in static_assert's first argument is false.

Like the #error preprocessor directive static_assert is a compile-time matter that doesn't have any effect on the run-time efficiency of the code in which it is used.

21.11: Numeric limits

The disadvantage of the limits defined in climits is that they are fixed limits. Let's assume you write a function template that receives an argument of a certain type. E.g,

    template<typename Type>
    Type operation(Type &&type);

How to proceed?

Since the constants in climits can only be used if the type to use is already known, the only approach seems to be to create function template specializations for the various integral types, like:

    template<>
    int operation<int>(int &&type)
    {
        return type < 0 ? INT_MIN : INT_MAX;
    }

The facilities provided by numeric_limits provide an alternative. To use these facilities the header file <limits> header file must be included.

The class template numeric_limits offers various members answering all kinds of questions that could be asked of numeric types. Before introducing these members, let's have a look at how we could implement the operation function template as just one single function template:

    template<typename Type>
    Type operation(Type &&type)
    {
        return
            not numeric_limits<Type>::is_integer ? 0 :
            type < 0 ? numeric_limits<Type>::min() :
                       numeric_limits<Type>::max();
    }

Here is an overview of the facilities offered by numeric_limits. Note that the member functions defined by numeric_limits return constexpr values. A member `member' defined by numeric_limits for type Type can be used as follows:

    numeric_limits<Type>::member    // data members
    numeric_limits<Type>::member()  // member functions

• Type denorm_min():

  if available for Type: its minimum positive denormalized value; otherwise it returns numeric_limits<Type>::min().

• int digits:

  the number of non-sign bits used by Type values, or (floating point types) the number of digits in the mantissa are returned.

• int digits10:

  the number of digits that are required to represent a Type value without changing it.

• Type constexpr epsilon():

  The difference for Type between the smallest value exceeding 1 and 1 itself.

• float_denorm_style has_denorm:

  denormalized floating point value representations use a variable number of exponent bits. The has_denorm member returns information about denormalized values for type Type:

  • denorm_absent: Type does not allow denormalized values;
  • denorm_indeterminate: Type may or may not use denormalized values; the compiler cannot determine this at compile-time;
  • denorm_present: Type uses denormalized values;

• bool has_denorm_loss:

  true if a loss of accuracy was detected as a result of using denormalization (rather than being an inexact result).

• bool has_infinity:

  true if Type has a representation for positive infinity.

• bool has_quiet_NaN:

  true if Type has a representation for a non-signaling `Not-a-Number' value.

• bool has_signaling_NaN:

  true if Type has a representation for a signaling `Not-a-Number' value.

• Type constexpr infinity():

  if available for Type: its positive infiniy value.

• bool is_bounded:

  true if Type contains a finite set of values.

• bool is_exact:

  true if Type uses an exact representation.

• bool is_iec559:

  true if Type uses the IEC-559 (IEEE-754) standard. Such types always return true for has_infinity, has_quiet_NaN and has_signaling_NaN, while infinity(), quiet_NaN() and signaling_NaN() return non-zero values.

• bool is_integer:

  true if Type is an integral type.

• bool is_modulo:

  true if Type is a `modulo' type. Values of modulo types can always be added, but the addition may `wrap around' producing a smaller Type result than either of the addition's two operands.

• bool is_signed:

  true if Type is signed.

• bool is_specialized:

  true for specializations of Type.

• Type constexpr lowest():

  Type's lowest finite value representable by Type: no other finite value smaller than the value returned by lowest exists. This value equals the value returned by min except for floating-point types.

• T constexpr max():

  Type's maximum value.

• T constexpr min():

  Type's minimum value. For denormalized floating point types the minimum positive normalized value.

• int max_exponent:

  maximum positive integral value for the exponent of a floating point type Type producing a valid Type value.

• int max_exponent10:

  maximum integral value for the exponent that can be used for base 10, producing a valid Type value.

• int min_exponent:

  minimum negative integral value for the exponent of a floating point type Type producing a valid Type value.

• int min_exponent10:

  minimum negative integral value for the exponent that can be used for base 10, producing a valid Type value.

• Type constexpr quiet_NaN():

  if available for Type: its a non-signaling `Not-a-Number' value.

• int radix:

  if Type is an integral type: base of the representation; if Type is a floating point type: the base of the exponent of the representation.

• Type constexpr round_error():

  the maximum rounding error for Type.

• float_round_style round_syle:

  the rounding style used by Type. It has one of the following enum float_round_style values:

  • round_toward_zero: values are rounded toward zero;
  • round_to_nearest: values are rounded to the nearest representable value;
  • round_toward_infinity:values are rounded toward infinity;
  • round_toward_neg_infinity: if it rounds toward negative infinity;
  • round_indeterminate: if the rounding style is indeterminable at compile-time.

• Type constexpr signaling_NaN():

  if available for Type: its a signaling `Not-a-Number' value.

• bool tinyness_before:

  true if Type allows tinyness to be detected before rounding.

• bool traps:

  true if Type implements trapping.

21.12: Polymorphous wrappers for function objects

To solve this problem polymorphous (function object) wrappers can be used. Polymorphous wrappers refer to function pointers, member functions or function objects, as long as their parameters match in type and number.

Before using polymorphic function wrappers the header file `<functional>' must be included.

Polymorphic function wrappers are made available through the std::function class template. Its template argument is the prototype of the function to create a wrapper for. Here is an example of the definition of a polymorphic function wrapper that can be used to point to a function expecting two int values and returning an int:

    std::function<int (int, int)> ptr2fun;

Such a function wrapper can now be used to point to any function the wrapper was created for. E.g., `plus<int> add' creates a functor defining an int operator()(int, int) function call member. As this qualifies as a function having prototype int (int, int), our ptr2fun may point to add:

    ptr2fun = add;

If ptr2fun does not yet point to a function (e.g., it is merely defined) and an attempt is made to call a function through it a `std::bad_function_call' exception is thrown. Also, a polymorphic function wrapper that hasn't been assigned to a function's address represents the value false in logical expressions (as if it had been a pointer having value zero):

    std::function<int(int)> ptr2int;

    if (not ptr2int)
        cout << "ptr2int is not yet pointing to a function\n";

Polymorphous function wrappers can also be used to refer to functions, functors or other polymorphous function wrappers having prototypes for which standard conversions exist for either parameters or return values. E.g.,

    bool predicate(long long value);

    void demo()
    {
        std::function<int(int)> ptr2int;

        ptr2int = predicate;    // OK, convertible param. and return type

        struct Local
        {
            short operator()(char ch);
        };

        Local object;

        std::function<short(char)> ptr2char(object);

        ptr2int = object;       // OK, object is a functor whose function
                                //  operator has a convertible param. and
                                // return type.
        ptr2int = ptr2char;     // OK, now using a polym. funct. wrapper
    }

21.13: Compiling template definitions and instantiations

    template <typename Container, typename Type>
    Type add(Container const &container, Type init)
    {
        return std::accumulate(container.begin(), container.end(), init);
    }

The calls container.begin() and container.end() are said to depend on template type parameters. The compiler, not having seen container's interface, cannot check whether container actually has members begin and end returning input iterators.

On the other hand, std::accumulate itself is independent of any template type parameter. Its arguments depend on template parameters, but the function call itself isn't. Statements in a template's body that are independent of template type parameters are said not to depend on template type parameters.

When the compiler encounters a template definition, it verifies the syntactic correctness of all statements not depending on template parameters. I.e., it must have seen all class definitions, all type definitions, all function declarations etc. that are used in those statements. If the compiler hasn't seen the required definitions and declarations then it will reject the template's definition. Therefore, when submitting the above template to the compiler the header file numeric must first have been included as this header file declares std::accumulate.

With statements depending on template parameters the compiler cannot perform those extensive syntactic checks. It has no way to verify the existence of a member begin for the as yet unspecified type Container. In these cases the compiler performs superficial checks, assuming that the required members, operators and types eventually become available.

The location in the program's source where the template is instantiated is called its point of instantiation. At the point of instantiation the compiler deduces the actual types of the template's parameters. At that point it checks the syntactic correctness of the template's statements that depend on template type parameters. This implies that the compiler must have seen the required declarations only at the point of instantiation. As a rule of thumb, you should make sure that all required declarations (usually: header files) have been read by the compiler at every point of instantiation of the template. For the template's definition itself a more relaxed requirement can be formulated. When the definition is read only the declarations required for statements not depending on the template's type parameters must have been provided.

21.14: The function selection mechanism

Assume we ask the compiler to compile the following main function:

    int main()
    {
        process(3, 3);
    }

    template <typename T>
    void process(T &t1, int i);                 // 1

    template <typename T1, typename T2>
    void process(T1 const &t1, T2 const &t2);   // 2

    template <typename T>
    void process(T const &t, double d);         // 3

    template <typename T>
    void process(T const &t, int i);            // 4

    template <>
    void process<int, int>(int i1, int i2);     // 5

    void process(int i1, int i2);               // 6

    void process(int i, double d);              // 7

    void process(double d, int i);              // 8

    void process(double d1, double d2);         // 9

    void process(std::string s, int i)          // 10

    int add(int, int);                          // 11

• First, a set of candidate functions is constructed. This set contains all functions that:
  • are visible at the point of the call;
  • have the same names as the called function.
  As function 11 has a different name, it is removed from the set. The compiler is left with a set of 10 candidate functions.

• Second, the set of viable functions is constructed. Viable functions are functions for which type conversions exist that can be applied so as to match the types of the function's parameters to the types of the actual arguments.

  This implies that at least the number of arguments must match the number of parameters of the viable functions. Function 10's first argument is a string. As a string cannot be initialized by an int value no approprate conversion exists and function 10 is removed from the list of candidate functions. double parameters can be retained. Standard conversions do exists for ints to doubles, so all functions having ordinary double parameters can be retained. Therefore, the set of viable functions consists of functions 1 through 9.

21.15: Determining the template type parameters

It may use any of the three standard template parameter transformation procedures (cf. section 21.4) when trying to match actual types to template type parameters. In this process it concludes that no type can be determined for the T in function 1's T &t1 parameter as the argument 3 is a constant int value. Thus function 1 is removed from the list of viable functions. The compiler is now confronted with the following set of potentially instantiated function templates and ordinary functions:

    void process(T1 [= int] const &t1, T2 [= int] const &t2);   // 2
    void process(T [= int] const &t, double d);                 // 3
    void process(T [= int] const &t, int i);                    // 4
    void process<int, int>(int i1, int i2);                     // 5
    void process(int i1, int i2);                               // 6
    void process(int i, double d);                              // 7
    void process(double d, int i);                              // 8
    void process(double d1, double d2);                         // 9

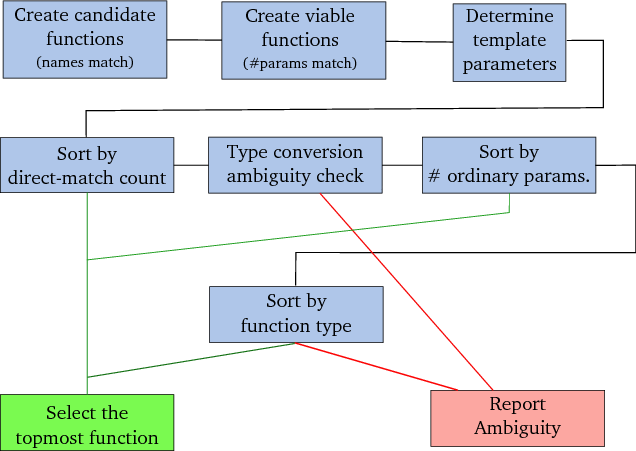
The compiler associates a direct match count value to each of the viable functions. The direct match count counts the number of arguments that can be matched to function parameters without an (automatic) type conversion. E.g., for function 2 this count equals 2, for function 7 it is 1 and for function 9 it is 0. The functions are now (decrementally) sorted by their direct match count values:

                                                             match
                                                             count
    void process(T1 [= int] const &t1, T2 [= int] const &t2);  2 // 2
    void process(T [= int] const &t, int i);                   2 // 4
    void process<int, int>(int i1, int i2);                    2 // 5
    void process(int i1, int i2);                              2 // 6
    void process(T [= int] const &t, double d);                1 // 3
    void process(int i, double d);                             1 // 7
    void process(double d, int i);                             1 // 8
    void process(double d1, double d2);                        0 // 9

When multiple functions appear at the top the compiler verifies that no ambiguity has been encountered. An ambiguity is encountered if the sequences of parameters for which type conversions were (not) required differ. As an example consider functions 3 and 8. Using D for `direct match' and C for `conversion' the arguments match function 3 as D,C and function 8 as C,D. Assuming that 2, 4, 5 and 6 were not available, then the compiler would have reported an ambiguity as the sequences of argument/parameter matching procedures differ for functions 3 and 8. The same difference is encountered comparing functions 7 and 8, but no such difference is encountered comparing functions 3 and 7.

At this point there is a draw for the top value and the compiler proceeds with the subset of associated functions (functions 2, 4, 5 and 6). With each of these functions an `ordinary parameter count' is associated counting the number of non-template parameters of the functions. The functions are decrementally sorted by this count, resulting in:

                                                         ordin. param.
                                                             count
    void process(int i1, int i2);                              2 // 6
    void process(T [= int] const &t, int i);                   1 // 4
    void process(T1 [= int] const &t1, T2 [= int] const &t2);  0 // 2
    void process<int, int>(int i1, int i2);                    0 // 5

Had function 6 not been defined, function 4 would have been used. Assuming that neither function 4 nor function 6 had been defined, the selection process would continue with functions 2 and 5:

                                                         ordin. param.
                                                             count
    void process(T1 [= int] const &t1, T2 [= int] const &t2);  0 // 2
    void process<int, int>(int i1, int i2);                    0 // 5

In this situation a draw is encountered once again and the selection process continues. A `type of function' value is associated with each of the functions having the highest ordinary parameter count and these functions are decrementally sorted by their type of function values. Value 2 is associated to ordinary functions, value 1 to template explicit specializations and value 0 to plain function templates.

If there is no draw for the top value the corresponding function is selected and the function selection process is completed. If there is a draw the compiler reports an ambiguity and cannot determine which function to call. Assuming only functions 2 and 5 existed then this selection step would have resulted in the following ordering:

                                                           function
                                                             type
    void process<int, int>(int i1, int i2);                    1 // 5
    void process(T1 [= int] const &t1, T2 [= int] const &t2);  0 // 2

• The set of candidate functions is constructed: identical names;
• The set of viable functions is constructed: correct number of parameters and available type conversions;
• Template type determination, dropping templates whose type parameters cannot be determined;
• Decrementally sort the functions by their direct match count values. If there is no draw for the top value the associated function is selected, completing the selection process.
• Inspect the functions associated with the top value for ambiguities in automatic type conversion sequences. If different sequences are encountered report an ambiguity and terminate the selection process.
• Decrementally sort the functions associated with the top value by their ordinary parameter count values. If there is no draw for the top value the associated function is selected, completing the selection process.
• Decrementally sort the functions associated with the top value by their function type values using 2 for ordinary functions, 1 for template explicit specializations and 0 for plain function templates. If there is no draw for the top value the associated function is selected, completing the selection process.
• Report an ambiguity and terminate the selection process.

21.16: SFINAE: Substitution Failure Is Not An Error

    struct Int
    {
        typedef int type;
    };

    template <typename Type>
    void func(typename Type::type value)
    {
    }

But templates may be overloaded and our next definition is:

    template <typename Type>
    void func(Type value)
    {}

But as we've seen in the previous section when the compiler determines which template to instantiate it creates a list of viable functions by matching the parameter types of available function prototypes with the provided actual argument types. To do so it has to determine the types of the parameters and herein lies a problem.

When evaluating Type = int the compiler encounters the prototypes func(int::type) (first template definition) and func(int) (second template definition). But there is no int::type, and so in a way this generates an error. However, the error results from substituting the provided template type argument into the various template definitions.

A type-problem caused by substituting a type in a template definition is not considered an error, but merely an indication that that particular type cannot be used in that particular template. The template is therefore removed from the list of candidate functions.

This principle is known as substitution failure is not an error (SFINAE) and it is often used by the compiler to select not only a simple overloaded function (as shown here) but also to choose among available template specializations (see also chapters 22 and 23).

21.17: Summary of the template declaration syntax

Not every template declaration may be converted into a template definition. If a definition may be provided it is explicitly mentioned.

• A plain template declaration (a definition may be provided):

  template <typename Type1, typename Type2>
  void function(Type1 const &t1, Type2 const &t2);
  

• A template instantiation declaration (no definition may be provided):

  template
  void function<int, double>(int const &t1, double const &t2);
  

• A template using explicit types (no definition may be provided):

  void (*fp)(double, double) = function<double, double>;
  void (*fp)(int, int) = function<int, int>;
  

• A template explicit specialization (a definition may be provided):

  template <>
  void function<char *, char *>(char *const &t1, char *const &t2);
  

• A template declaration declaring friend function templates within class templates (covered in section 22.10, no definition may be provided):

  friend void function<Type1, Type2>(parameters);
  

21.18: C++14: variable templates

A variable template starts with a familiar template header, followed by the definition of the variable itself. The template header specifies a type, for which a default type may also be specified. E.g.,

    template<typename T = long double>
    constexpr T pi = T(3.1415926535897932385);

To use this variable a type must be specified, and as long as the initialized value can be converted to the specified type the conversion is silently performed by the compiler:

    cout << pi<> << ' ' << pi<int>;

Specializations are also supported. E.g., to show the text `pi' a specialization for a char const * type can be defined:

    template<>
    constexpr char const *pi<char const *> = "pi";

• Table of Contents
• Previous Chapter
• Next Chapter